Welcome to Electrostatics Zone! Here we collect the work done on molecular electrostatics at the IIT group led by Walter Rocchia. In this site you can read about our research, publications and developed software, which you are welcome to download and try. To download some of our software you will need a very light registration, so as that we can keep you updated when a new release comes out.
Electrostatics plays a key role at the molecular scale and especially in Biochemistry. A few examples are: the estimation of the solvation free energy of a bio-molecular system, protein-ligand, protein-protein and protein-DNA interaction, pKa, protein structure. Implicit solvent modeling is a possible strategy for describing these phenomena. This approach can be justified in the context of classical continuum electrostatics and by a mean field approximation of the effects of the ionic solution consistent with the rules of statistical mechanics. Despite a certain degree of approximation, implicit methods are still of wide interest because of their algorithmic efficiency, due to the reduced number of degrees of freedom, and a relatively good compromise between model accuracy and efficiency. Among them, the Poisson-Boltzmann equation (PBE) approach is able to best capture the effects of the complex shapes arising at the nanoscale.
We are part of the development team of DelPhi, a well known Poisson-Boltzmann equation solver. Our research mainly focuses on geometrical and biophysical aspects of the molecular surface as well as algorithm and model improvements of the PBE numerical solution. We are also interested in a more general application of the PBE to systems at the nano/mesoscale. Our activity has been partially funded by NIGMS, NIH through grant contract, 1R01GM093937-01.
Poisson-Boltzmann equation and its solution:
Biomolecular systems are composed of biological macromolecules, proteins and nucleic acids, and of a number of small organic molecules and electrolytes immersed in aqueous solution. The role of the solvent is sometimes crucial because of the effects it can have on the behavior of the biomolecules while performing their function. In Computational Biological Chemistry, the so called implicit solvent models provide an estimate of the average solvent effect, resulting in a huge computational saving, since the number of degrees of freedom of the solvent is
usually much larger than that of the solute. Approaches based on the Poisson-Boltzmannn Equation (PBE) [1] and the Generalized Born Approximation [2] are widely used to estimate the reaction of the media to the electric field generated by the partial charges on the solute.
Poisson-Boltzmann equation reads:
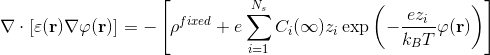
where e is the electron charge, Ci at infinity is the bulk concentration of the i-th ion type and zi is its valence, kB is the Boltzmann constant, T is the temperature, ρfixed represents the partial charge distribution and φ(r) the potential; ε(r) is the space varying dielectric constant, which is a direct consequence of the adopted surface definition. The solution of this equation is needed to acquire an accurate knowledge of the reaction field and it can also be used to derive the electrostatic forces exerted by the solvent on the solute, which are mostly located at the boundary between high and low dielectric regions, i.e. on the MS.
For these reason a key role on PB solution is given both in terms of accuracy and efficiency by the definition of the molecular surface and by the boundary conditions employed to solve the equation.